For a PDF version click here psk-and-fsk-over-fm.pdf

It is common for people to modulate an FM transmitter with PSK or FSK modulated audio on VHF/UHF. My feeling was this was not desirable due to efficiencies of various sorts but as FM transmitters are easy to create, can use nonlinear amplifies (unlike SSB), and ubiquitous, I wondered how bad is it really doing it this way and what sort of PSK/FSK modulation works best for a particular task.

To test how PSK and FSK performed over narrowband FM (NBFM) I simulated the following in Matlab.

I was interested in channels that were additive white Gaussian noise (AWGN) this is similar to line of sight communication using VHF/UHF frequencies. The FM transmitter had a deviation of 5 kHz whilst the FM receiver consisted of an 11 kHz bandpass filter followed by an FM discriminator. The simulation was performed in the passband with a carrier frequency of 12 kHz. The PSK/FSK demodulators had AGC and symbol tracking but did not have frequency tracking. For the PSK I used differential phase shift keying (DPSK), while not as efficient as coherent PSK it is easier to implement and used in HAM modes such as PSK31 which is actually differentially encoded. Of the simulation, the FM receiver was the object that I imagine could vary wildly from one hardware implementation to another.

As the FM transmitter is modulated with PSK/FSK what is transmitted over the air is clearly not PSK/FSK but is something else. For the HAM mode PSK31 I chose to denote this as DBPSK31/NBFM; DBPSK for differential binary phase shift keying, 31 bits per second, and sent over narrowband FM assuming an FM deviation of 5 kHz.

The Matlab simulation program I wrote can be obtained here
psk-and-fsk-simulations-matlab.zip.

To send information it takes energy (as in Joules), the amount of energy to send one bit of information is denoted as Eb. The amount of noise (power as in Watts) per Hz or noise density is denoted as No. The noise density is more useful than the noise N as it does not rely on the amount of bandwidth B_w (in Hz) you are listening to. When sending a bit there is a probability that the bit will become corrupted, this probability is called the bit error rate or BER.

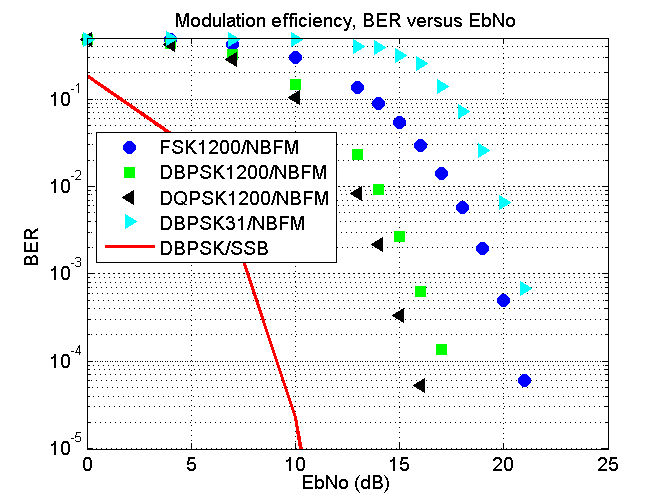
For a particular modulation scheme plotting BER versus Eb ⁄ No (written as EbNo) describes the energy required to send one bit of information given a noise density No and a desired BER. It tells you how much energy (not power) you are going to need to send one bit of information; this is on air energy efficiency. For a particular modulation scheme these BER versus EbNo plots are independent on how fast you send the information as doubling the throughput doubles the on air power and halves the time required hence the energy per bit which is time times power is unchanged. Therefore DBPSK31 has the same on air energy efficiency as DBPSK1200. From this one might think that DBPSK31/NBFM has the same on air energy efficiency as DBPSK1200/NBFM, but it doesn’t. The reason is the NBFM modulation is unchanged and DBPSK31/NBFM is a different modulation scheme than DBPSK1200/NBFM. Therefore we have to plot these on air energy efficiency plots for each PSK/FSK modulation that we feed into the MBFM transmitter; this is what is shown in the following figure.

This figure shows how much energy per bit you will need for a given bit error rate and noise. Points toward the left of the graph imply that one bit does not require a great deal of energy to send while points towards the right of the graph imply that one bit requires a great deal of energy to send. Points towards the bottom of the graph mean you will get few errors while points towards the top mean you will get many errors. Think, bottom left good, top right bad.

Sending PSK31 over an SSB receiver ideally results in the red curve. Sending the same PSK31 signal over NBFM results in the cyan squares according to my simulations. Any BER above 10^− 3 I would classify as useless and when I talk about EbNo and other such signal-to-noise ratios I consider about 10^− 5 to 10^− 4 the BER that is of interest to me. This being the case, for PSK31 one bit of on air energy sent over NBFM requires 10 dB more energy than if it was sent over SSB; that’s 10 J compared to 1 J. From the other modulation schemes we see that FSK1200/NBFM results in approximately the same EbNo of 21 dB as PSK31’s DBPSK31/NBFM. Using higher rates of PSK improves efficiency and increasing the constellation size from 2 to 4 (BPSK to QPSK) also seems to improve the efficiency a little.

That PSK/NBFM is more efficient than FSK/NBFM is no real surprise to me. However what was a bit of a surprise was DQPSK1200/NBFM seems slightly more efficient than DBPSK1200/NBFM this is back to front compared to what happens with DBPSK and DQPSK. Anyway what this figure shows is that PSK is more efficient FSK over NBFM when using the same rates. It also shows that PSK31/NBFM is basically the same as FSK1200/NBFM.

While energy efficiency is all very good, it quite often is not a major concern, particularly when one does not need to send a lot of information. what would you rather do, send a short sentence using a 1 kW transmitter taking 1 ms or the same message using a 1 W transmitter for 10 seconds? The energy required is 1 J and 10 J respectively. It’s clearly more efficient to use the 1 kW transmitter, but a 1 kW transmitter might be prohibitive. Personally I would be prepared to wait the 10 seconds.

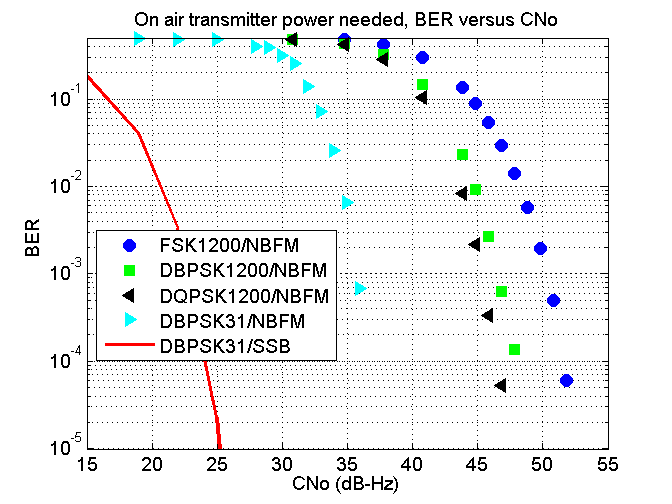
This brings us to the power of the transmitter you would need for a desired BER and No. You can split up energy Eb into time and power E_bf_b = C where f_b is the effective bit rate in Hz and C is the on air power. Therefore C ⁄ No = f_b(E_b ⁄ No). C ⁄ No is the carrier power to noise density ratio and is written as CNo. Plotting BER versus CNo describes the on air power required to send information given a noise density No and a desired BER. Therefore from this type of plot you can compare the on-air transmitter power requirement from one modulation scheme given it’s bit rate to another given its bit rate.

In the following graph I plot my simulation results of BER versus CNo for the different modulation schemes seen in the previous figure.

Once again considering a BER of around 10^− 5 to 10^− 4 as an acceptable level, FSK1200/NBFM needs the most amount of power and uses approximately 15 dB-Hz more than PSK31 over NBFM. This means if PSK31 over NBFM requires an NBFM FM transmitter of 1 W, then FSK1200 over NBFM requires an NBFM FM transmitter of 32 W.

Both DBPSK1200/NBFM and DQPSK1200/NBFM use around 5 dB-Hz less than FSK1200/NBFM.

Of the modulation schemes I tested, the on air energy efficiency of slow modulation schemes such as PSK31/NBFM is not particularly efficient and is comparable to FSK1200/NBFM. However the actual on air transmitter power needed is around 30 times less for PSK31/NBFM than FSK1200/NBFM. Therefore if the purpose of using the digital mode is to send a small amount of information the greatest distance with the least amount of power then PSK31/NBFM is the most appropriate choice of modulating NBFM of the schemes I tested. If the aim is to send large volumes of information through then DQPSK1200/NBFM might be a better alternative and is certainly better than FSK1200/NBFM.

Through the use of FEC and increasing the constellation size such as LDPC-DQPSK psk31-investigation the on air energy efficiency could be improved without increasing bit rate which would reduce the on air transmission power even further.

Using an SSB transmitter (or directly modulating RF) DBPSK was 6 dB more efficient than the closest NBFM efficiency rival found so far of DQPSK1200/NBFM. The difference in efficiency between DBPSK and FSK1200/NBFM was approximately double this at around 12 dB. Packet radio uses FSK1200/NBFM and by using this they need transmitters that are approximately four times more powerful compared to if they were to use DQPSK1200/NBFM according to my simulations.

Considering that FM transmitters are ubiquitous, making the most of these FM transmitters and optimizing the modulation schemes they use for the task at hand makes sense.

Jonti 2015
Home