An example into a procedure to solve matching network problems.
Definitions:
Frequency
(Frequency in hertz)
(L is inductance in Henrys)
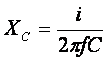(C is capacitance in Farads)
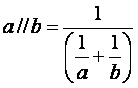(Parallel components function)
Properties of the parallel components function.
(Commutivity)
(Associativity)
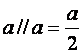(Double formula)
(Exchange formula)
Given 
then
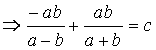(By def)
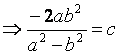
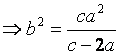
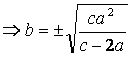(Lemma 1)
A Pi network.
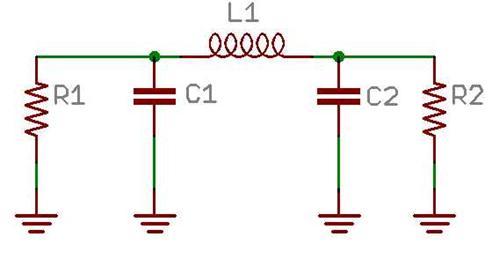
Given a Pi network, frequency and input and output resistances, it is possible to parameterize with one variable the three unknowns, L1,C1,C2.
I will choose C1 as my variable.
If we were to remove resistor one from the schematic and add up all the other components, for an exact impedance match these components must add up to the same value as resistor one. And vise versa for resistant two. This results in the two following formulae.
(I)
(II)
Make 
the
subject for both of these formulae using the exchange property.
(From I)
(III)
(From II) (IV)
Putting (III) and (IV) together we get
Using (Lemma 1) and solving for
we
get
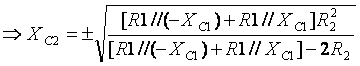
As the stuff inside the square root must be negative to create a purely imaginary number and a capacitor has a positive purely imaginary number, this implies we must take the positive square root.
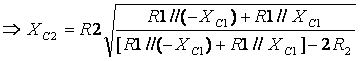
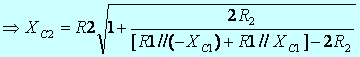
Now we have 
,
we have 
.
That is it as far as parameterization of this problem as a function of one variable.
Next step:
As my understanding, in electronics there is something called Q, which stands for quality. It seems to be related to bandwidth. One says the Q of this impedance matching circuit is something. I realize the smaller the Q the bigger the bandwidth and vice versa. Apparently, in this Pi network one can say...
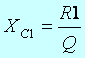
Then, with these three formulae in blue, it is possible given the situation we have known input and output impedances, and frequency with a certain Q, to find uniquely, the three reactive components of the pie network.
This page shows an example of an approach to solving reactive component matching network problems. You can probably see with more components, finding solutions could prove to be far more challenging.
Jonti
2006
Jonti 2006